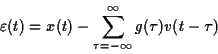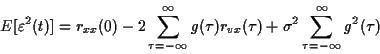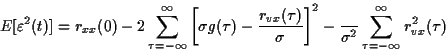Pour optimiser la sépartion d'un signal et d'un bruit de mesure
et atténuer les distorsions apportées par un filtre à un signal,
on a posé le problème de la manière suivante: On suppose qu'un
signal stationnaire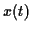 
de densité spectrale connue,
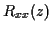est déformé et entâché d'un bruit de mesure stationnaire. Soit 
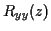la densité
spectrale, elle aussi connue, de ce signal 
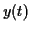, version déformée de 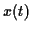. On connait
l'intercorrélation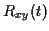 
entre les signaux 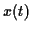et .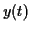
On cherche un filtre 
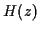dont la sortie sera 
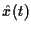de manière à
minimiser l'énergie
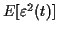de l'erreur entre le signal original 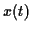et
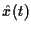sa prédiction à partir du signal filtré (cf fig. 68)
 |
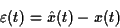(319) |
.
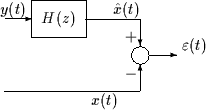
Figure 68:
Schéma du filtrage de Wiener
 |
Nous supposerons que 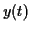a été engendré par un bruit blanc 
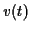de variance 
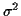filtré par un filtre linéaire causal et
stable dont la réponse impulsionnelle a pour transformée en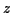 
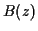. On peut
écrire 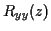sous la forme
 |
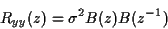(320) |
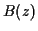( est appelé ``facteur spectral'' de 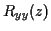, cf le paragraphe
7.3.13).
Ce filtre 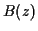a un inverse 
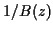qui est lui aussi
causal et stable.
La recherche du filtre 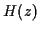se ramène alors à
la recherche d'un filtre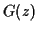 
dont la réponse impulsionnelle est
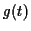
Figure 69:
Blanchiment du signal 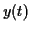ramenant le calcul de 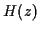au calcul de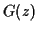
 |
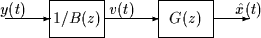L'erreur de prédiction
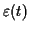peut alors s'écrire
 |
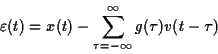(321) |
La variance de
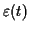peut s'écrire alors en fonction 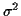de
, de 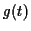, de
la variance de 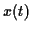, soit 
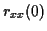et de l'intercorrélation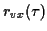 
 |
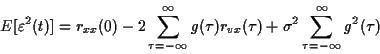(322) |
qu'on peut réécrire
 |
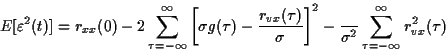(323) |
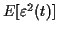est minimale lorsque
 |
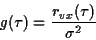(324) |
soit si on exprime cette relation en termes de transformées en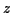
 |
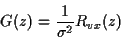(325) |
où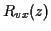 
est la transformée en 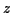de
).
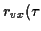On peut exprimer 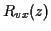en fonction de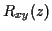 
 |
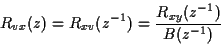(326) |
et
 |
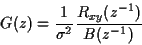(327) |
En divisant par 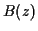, on obtient le filtre cherché
 |
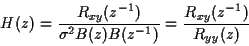(328) |
Toutefois, ce filtre n'est pas nécessairement réalisable, car il
n'est pas nécessairement causal.
Sous-sections
[ Table des matières ]