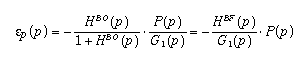Soit e(t) l'écart entre la consigne c(t) et la sortie obtenue y(t). On s'intéresse en général au régime établi et à la valeur finale de cet écart quand t®¥, que l'on appelle erreur statique.
La valeur de e¥ , quand la consigne est unitaire, exprimée en pourcents, constitue la précision du système.
Pour un système asservi à retour unitaire, comportant une consigne de transformée de Laplace C(p) et une perturbation de transformée de Laplace P(p), dont on suppose connu le point d'application :
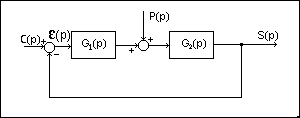
on obtient :
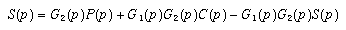
Puisque :
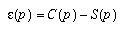
et
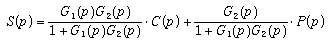
avec la notation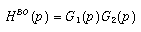 
, on obtient l'expression suivante pour l'écart e(p) :
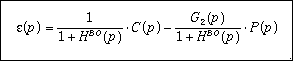
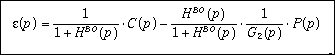
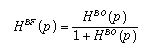
L'écart e(p) à chaque instant est la somme de deux termes :
un écart relatif à la consigne :
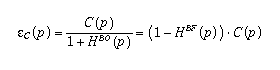
un écart dû à la perturbation :
