La loi de Bernouilli
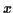 prend la valeur
prend la valeur 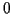 avec la probabilité
avec la probabilité 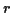 et la valeur
et la valeur 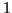 avec la probabilité
avec la probabilité 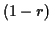 . Comme toute variable aléatoire
discrète, elle ne possède pas de densité de probabilité, il faut
avoir recours à la distribution de Dirac
. Comme toute variable aléatoire
discrète, elle ne possède pas de densité de probabilité, il faut
avoir recours à la distribution de Dirac
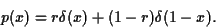 |
(20) |
Loi uniforme
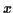 prend des valeurs uniquement dans l'intervalle
prend des valeurs uniquement dans l'intervalle 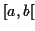 . Sa
densité de probabilité est nulle en dehors de cet intervalle et
y vaut
. Sa
densité de probabilité est nulle en dehors de cet intervalle et
y vaut
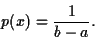 |
(21) |
Figure 6:
Densité de probabilité de la loi uniforme :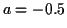 ,
,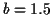
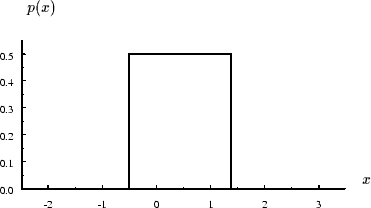 |
Sa fonction de répartition est composée de trois segments de
droites
Loi normale ou gaussienne
Sa densité de probabilité est
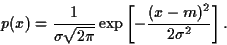 |
(23) |
Figure 7:
Densité de probabilité de la loi gaussienne
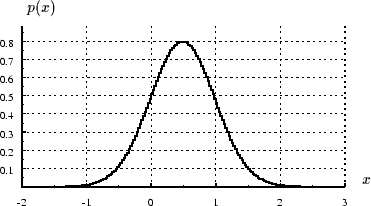 |
La densité de probabilité passe par son maximum pour 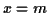 . Elle a
ses points d'inflexion en
. Elle a
ses points d'inflexion en 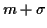 et
et 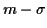 .
.
Cette loi présente trois caractéristiques importantes :
 Elle
permet des développements mathématiques efficaces, en particulier
en ce qui concerne les variables aléatoires indépendantes parce
qu'elle s'exprime comme l'exponentielle d'une forme quadratique
(ceci sera précisé lorsque nous présenterons l'analyse des couples de variables
aléatoires.
Elle
permet des développements mathématiques efficaces, en particulier
en ce qui concerne les variables aléatoires indépendantes parce
qu'elle s'exprime comme l'exponentielle d'une forme quadratique
(ceci sera précisé lorsque nous présenterons l'analyse des couples de variables
aléatoires.
 Toute l'information est donnée
directement par les paramètres
Toute l'information est donnée
directement par les paramètres  et
et 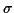 qui caractérisent
respectivement la valeur moyenne et la dispersion autour de cette
valeur moyenne.
qui caractérisent
respectivement la valeur moyenne et la dispersion autour de cette
valeur moyenne.
 Enfin, c'est la loi qu'on obtient naturellement en
additionnant un grand nombre de variables aléatoires
indépendantes; elle représente bien un grand nombre de phénomènes
physiques aléatoires comme le bruit de fond, les erreurs entâchant
les mesures, etc...
Enfin, c'est la loi qu'on obtient naturellement en
additionnant un grand nombre de variables aléatoires
indépendantes; elle représente bien un grand nombre de phénomènes
physiques aléatoires comme le bruit de fond, les erreurs entâchant
les mesures, etc...
Loi de Poisson
C'est la loi qu'on obtient en comptant des évènements aléatoires
indépendants: arrivée d'une particule sur un capteur, décompte
des appels sur un central téléphonique, comptage de voitures sur
une route, etc.. C'est la loi centrale des études sur les files
d'attente dans les réseaux de communication. Elle dépend d'un
paramètre 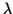 qui caractérise le débit moyen du flux. La
probabilité d'observer
qui caractérise le débit moyen du flux. La
probabilité d'observer 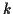 événements pendant une durée
événements pendant une durée 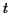 est
donnée par
est
donnée par
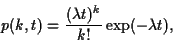 |
(24) |
pour 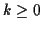 et
et 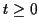 , où on prend
, où on prend 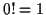 .
.
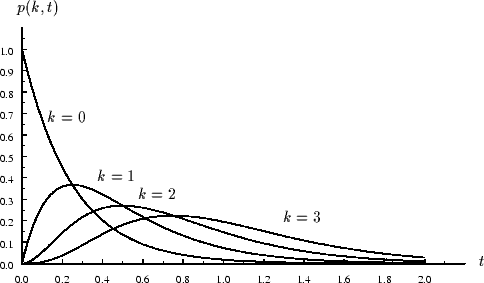
Figure 8:
Densités de probabilités  de la loi de Poisson
de la loi de Poisson
 |
[ Table des matières ]


