La probabilité que 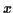 appartienne à l'intervalle
appartienne à l'intervalle 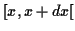 est
est
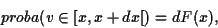 |
(14) |
et si 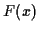 est différentiable,
est différentiable,
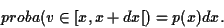 |
(15) |
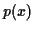 , densité de probabilité de la variable aléatoire
, densité de probabilité de la variable aléatoire 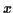 est ainsi la dérivée de la fonction de répartition
est ainsi la dérivée de la fonction de répartition 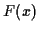 .
.
Figure:
Exemple de densité de probabilité, la loi de Cauchy:
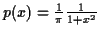
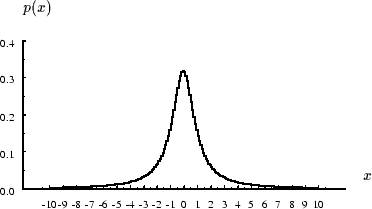 |
C'est
une fonction non négative mais ce n'est pas une probabilité, elle
n'est pas nécessairement inférieure à 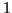 . (Dans de nombreux
ouvrages, on conserve la notation
. (Dans de nombreux
ouvrages, on conserve la notation 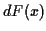 , plus cohérente, qui
tient compte des éventuelles discontinuités de la fonction de
répartition. On peut estimer la densité de probabilité en
construisant un histogramme pour lequel le pas d'échantillonnage
de l'axe des réels est infiniment petit et le nombre d'expériences
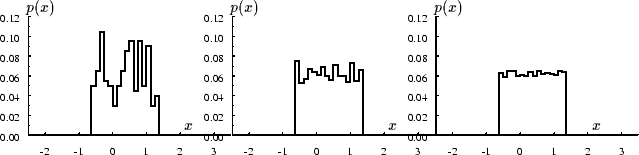
infiniment grand. Dans l'exemple de la figure 5,
le nombre d'échantillons
est de 2000, ensuite 20 000 et enfin 200 000.
, plus cohérente, qui
tient compte des éventuelles discontinuités de la fonction de
répartition. On peut estimer la densité de probabilité en
construisant un histogramme pour lequel le pas d'échantillonnage
de l'axe des réels est infiniment petit et le nombre d'expériences
infiniment grand. Dans l'exemple de la figure 5,
le nombre d'échantillons
est de 2000, ensuite 20 000 et enfin 200 000.
Figure 5:
Convergence de l'histogramme vers la densité de probabilité
 |
[ Table des matières ]