Fonction de répartition

On définit la fonction de répartition qui est la fonction

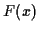donnant la probabilité pour que la valeur mesurée

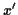soit strictement inférieure à

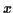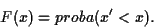(13)

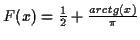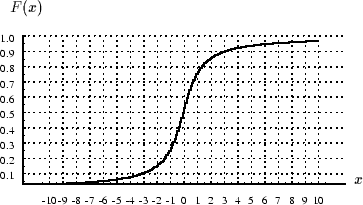La figure 2 donne un exemple de fonction de répartition pour la loi de Cauchy où

**Figure 2:** Exemple de fonction de répartition, la loi de Cauchy

C'est une fonction non décroissante qui peut présenter des paliers et des discontinuités (à droite). Elle est continue à gauche. Elle tend vers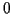

lorque

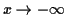et vers

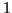lorsque

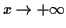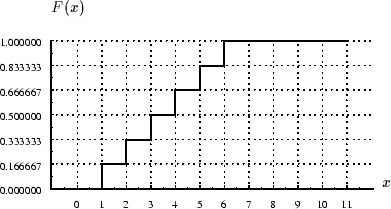**Figure 3:** Fonction de répartition pour le lancer de dé

Il est parfois intéressant de penser à étudier la fonction de répartition pour trouver la solution de certains problèmes élémentaires.