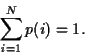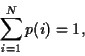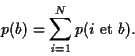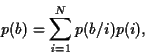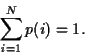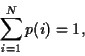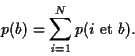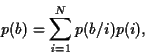On considère un ensemble de 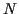 événements possibles, par exemple les six
résultats possibles d'un lancer de dé. On assigne un numéro à
chacun de ces
événements possibles, par exemple les six
résultats possibles d'un lancer de dé. On assigne un numéro à
chacun de ces 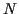 événements. On associe à chacun de ces
événements élémentaires un nombre positif ou nul
événements. On associe à chacun de ces
événements élémentaires un nombre positif ou nul 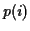 appelé probabilité qui est la
proportion entre le nombre de fois où ce résultat apparait et le
nombre total d'expériences. La somme des
appelé probabilité qui est la
proportion entre le nombre de fois où ce résultat apparait et le
nombre total d'expériences. La somme des 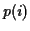 sur l'ensemble des
expériences vérifie :
sur l'ensemble des
expériences vérifie :
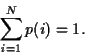 |
(1) |
Ceci traduit le fait que le résultat de l'expérience fera toujours
partie des 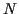 événements possibles.
Les
événements possibles.
Les 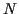 événements sont mutuellement exclusifs ou disjoints : ils ne peuvent se
réaliser simultanément. On ne peut obtenir à la fois un et trois
lorqu'on lance un dé. Ou bien, si dans le couple
événements sont mutuellement exclusifs ou disjoints : ils ne peuvent se
réaliser simultanément. On ne peut obtenir à la fois un et trois
lorqu'on lance un dé. Ou bien, si dans le couple  ,
, 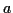 représente le résultat
d'un tirage à pile ou face (
représente le résultat
d'un tirage à pile ou face (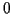 ou
ou 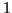 ) et
) et 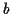 le résultat d'un
lancer de dé, les événements
le résultat d'un
lancer de dé, les événements 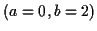 et
et 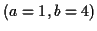 sont
disjoints. Si deux événements sont disjoints, la
probabilité que l'un ou l'autre se réalise est
sont
disjoints. Si deux événements sont disjoints, la
probabilité que l'un ou l'autre se réalise est
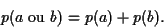 |
(2) |
Les résultats 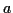 et
et 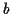 de deux expériences sont indépendants si
la probabilité de les obtenir simultanément est
de deux expériences sont indépendants si
la probabilité de les obtenir simultanément est
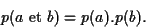 |
(3) |
Si par exemple, un lancer de dé et un tirage à pile ou face sont indépendants,
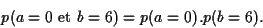 |
(4) |
La décomposition d'un événement en événements disjoints permet
d'écrire le théorème des probabilités totales
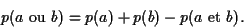 |
(5) |
La mise en évidence de la dépendance au sens des probabilés est
fondamentale dans les application: dans de nombreux problèmes, lorsqu'on tente de faire des prédictions, il est
essentiel de pouvoir dire si le résutat d'une expérience  peut
dépendre d'un autre phénomène
peut
dépendre d'un autre phénomène 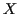 . Dans l'affirmative, il faut pouvoir
préciser l'effet de
. Dans l'affirmative, il faut pouvoir
préciser l'effet de 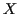 sur
sur  .
Cette notion de dépendance nécessite la définition des
probabilité conditionnelles: la probabilité que
.
Cette notion de dépendance nécessite la définition des
probabilité conditionnelles: la probabilité que 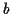 se réalise
sanchant que
se réalise
sanchant que 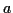 s'est réalisé est
s'est réalisé est
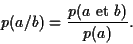 |
(6) |
Cette notion de probabilité conditionnelle est la base de la
prédiction au sens statistique du résultat d'une expérience. On
peut par exemple donner la probabilité qu'une des ``causes''
parmi 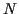 causes possibles d'un événement
causes possibles d'un événement 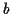 soit celle qui a
effectivement produit l'effet mesuré:
On suppose que les
soit celle qui a
effectivement produit l'effet mesuré:
On suppose que les 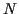 causes possibles
causes possibles  sont
mutuellement exclusives et qu'on les connait toutes (il n'y a pas
d'autres causes possibles). On connait la probabilité de chacune
d'entre elles,
sont
mutuellement exclusives et qu'on les connait toutes (il n'y a pas
d'autres causes possibles). On connait la probabilité de chacune
d'entre elles, 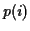 , qui vérifie
, qui vérifie
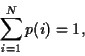 |
(7) |
car on connait toutes les causes.
On connait aussi les probabilités conditionnelles 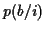 . La
probabilité que
. La
probabilité que 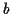 se réalise est
se réalise est
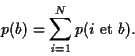 |
(8) |
En utilisant les deux écritures possibles de la formule donnant les probabilités conditionnelles,
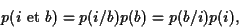 |
(9) |
on obtient d'une part,
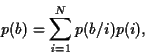 |
(10) |
et en éliminant 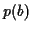 dans l'eq. :
dans l'eq. :
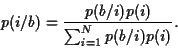 |
(11) |
Ce résultat est connu sous le nom de formule de Bayes.
Une notion couramment utilisée quand on étudie les probabilités conditionnelles est la
maximisation de fonction de vraisemblance: on recherche le
maximum sur tous les  de
de 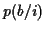 .
.
[ Table des matières ]