Si dans l'exemple précédent, au lieu de calculer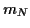 
, on étudie
 |
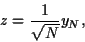(72) |
la relation entre les fonctions caractéristiques devient
 |
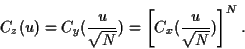(73) |
Le développement du logarithme de 
donne
 |
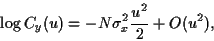(74) |
et donc
 |
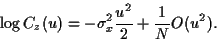(75) |
Lorsque
 |
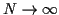
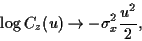(76) |
 |
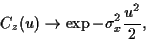(77) |
et en termes de densité de probabilité,
 |
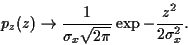(78) |
La somme d'un grand nombre de variables aléatoires indépendantes
de même loi tend vers une variable gaussienne
.
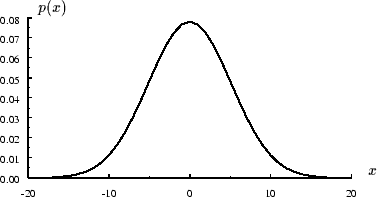
Figure 18:
La densité de probabilité de la somme d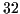e 
variables aléatoires indépendantes équiréparties
est très similaire à celle d'une gaussienne
 |
On peut généraliser ce résultat au cas où les variables ne sont pas de même loi et partiellement indépendantes. Ce qui justifie
l'utilisation des variables aléatoires gaussiennes pour
représenter les phénomènes aléatoires relativement complexes.
[ Table des matières ]