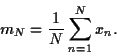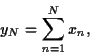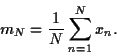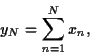Quand on estime une valeur, par exemple la moyenne d'une variable
aléatoire à partir du résultat de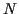 
expériences différentes, on
calcule une nouvelle variable aléatoire sous la forme
 |
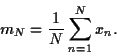(65) |
Nous supposerons que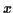 
est une variable aléatoire centrée et que
tous les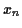 
suivent la même loi de probabilité. Pour étudier la
variance de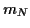 
, nous utiliserons la fonction caractéristique:
la variable
 |
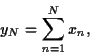(66) |
a pour fonction caractéristique
 |
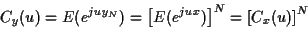(67) |
qu'on peut écrire en utilisant les logarithmes
 |
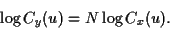(68) |
Nous supposons que 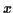est une variable aléatoire centrée. Le
premier terme du développement en série de Taylor donne
 |
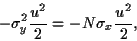(69) |
et la variance de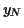 
est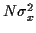 
. Comme 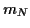est obtenue
en divisant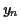 
par 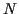la variance de 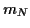vaut
 |
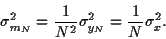(70) |
La relation entre les écarts-type est
 |
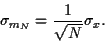(71) |
C'est une quantité qui tend vers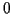 
lorsque
:
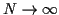l'incertitude sur le résultat décroit avec le nombre
d'expériences. Il faut cependant remarquer que cette décroissance
est très lente: pour améliorer la précision d'un facteur dix, il
faut multiplier le nombre d'expériences par cent.
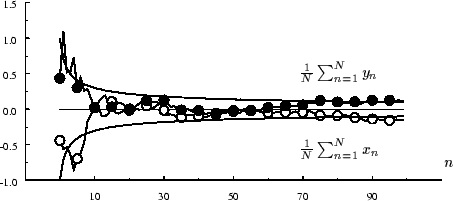
Figure 17:
Evolution de la moyenne de 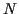réalisations de deux
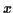variables aléatoires, et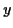 
, en fonction de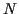
 |
[ Table des matières ]