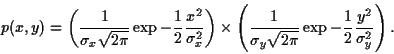La densité de probabilté d'un couple de variables aléatoires
centrées
gaussiennes dans leur ensemble est donnée par
 |
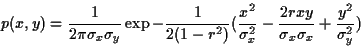(60) |
formule qui fait apparaître les variances de chacune des deux
variables ainsi que leur coefficient de corrélation; on notera que
l'exposant de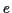 
est une forme quadratique définie positive
lorsque 
.
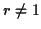Figure 15:
Densité de probabilité d'un couple de variables aléatoires gaussiennes
 |
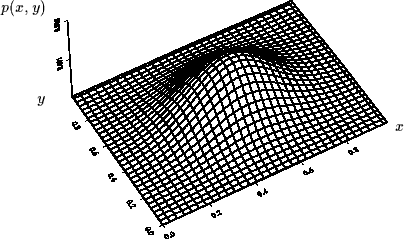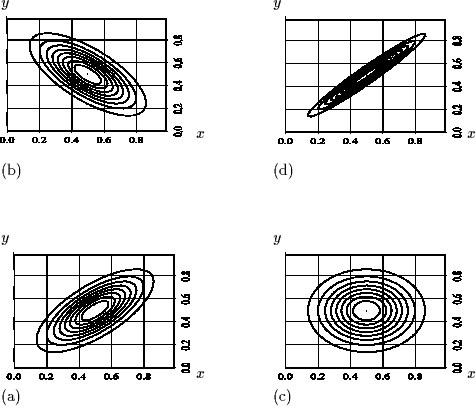
Figure 16:
Courbes de niveau de la densité de probabilité d'un couple de variables aléatoires gaussiennes
: le coefficient de corrélation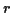 
prend pour valeur (a) 
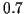, (b)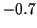 
(corrélation négative) , (c) 
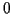(indépendance), (d) 
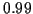(corrélation forte)
 |
Si le coefficient 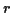est nul, 
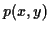s'écrit comme un produit
 |
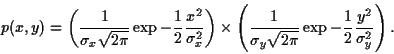(61) |
Les variables sont donc indépendantes.
Deux variables aléatoires
gaussiennes orthogonales sont nécessairement indépendantes.
On peut toujours représenter un couple de variables aléatoires
gaussiennes comme une combinaison linéaire de variables
aléatoires gaussiennes indépendantes.
Un changement de variables
par rotation
permet d'obtenir deux variables orthogonales (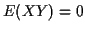
). Par
conséquent la densité du couple de variables aléatoires (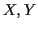
) 
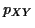se factorise sous la forme
 |
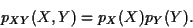(63) |
La densité de probabilité conditionnelle de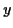 
connaissant 
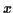s'écrit
 |
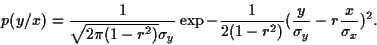(64) |
Lorsque 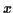est finé, 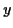est une variable aléatoire gaussienne
non centrée de moyenne
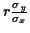et de variance
.
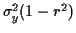La somme de deux variables aléatoires gaussiennes dont les variances sont respectivemen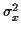t 
et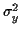 
et dont le coefficient de corrélation est 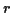est une variable
aléatoire gaussienne de variance
.
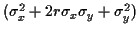[ Table des matières ]
