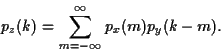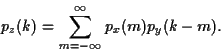Soient deux variables aléatoires indépendantes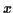 
et 
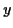prenant
des valeurs entières. La porbabilité pour que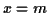 
et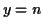 
simultanément est 
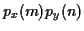. Soit 
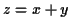. Sa densité de
probabilité est
 |
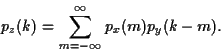(55) |
De manière générale la densité de probabilité de la somme s'écrit
sous la forme d'une convolution.
 |
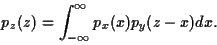(56) |
Par exemple si sont des variables aléatoires équiréparties entre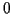 
et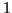 
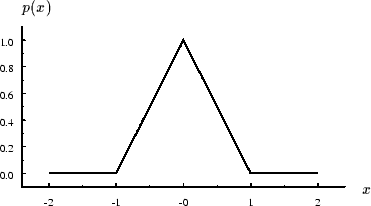
Figure 14:
Densité de probabilité de la somme de deux variables aléatoires indépendantes équiréparties
entre -1/2 et 1/2
 |
La fonction caractéristique de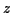 
est la transformée de Fourier
d'un produit de convolution. C'est donc le produit des fonctions
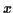caractéristiques de et :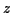
 |
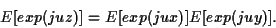(57) |
On en déduit que la moyenne des sommes la somme des moyennes est égale à
et que la variance de la somme est égale à la somme des variances
 |
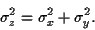(58) |
Cependant si les deux variables ne sont pas indépendantes, on peut
seulement écrire que
 |
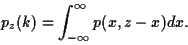(59) |
[ Table des matières ]