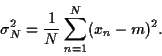La deuxième caractérisation importante d'une variable aléatoire
est sa dispersion autour de la valeur moyenne. On peut l'estimer
en calculant un ``moment d'inertie'' de la variable par rapport à
cette valeur moyenne. Par exemple à partir de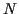 
mesures, on
calculera
 |
(30) |
Comme dans le cas de la moyenne, l'affinement de l'histogramme
lorsque tend vers l'infini
conduit à une formule faisant apparaître la densité de probabilité
 |
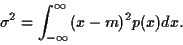(31) |
On l'écrit en fonction du moment du deuxième ordre
 |
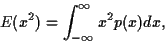(32) |
soit
 |
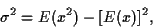(33) |
résultat obtenu par un développement de (31) où on
fait apparaitre l'expression (27) de la moyenne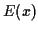 
.
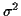est la ``variance'' de la variable aléatoire. Sa racine
carrée, 
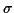est son écart-type. Cette quantité caractérise la
dispersion de la variable autour de la moyenne. Lorsque la
variance est nulle, la densité de probabilité est concentrée en un
point et la variable aléatoire est connue avec certitude.
La notion de variance est fondamentale dans un bon nombre
d'applications en particulier en traitement du signal, et aussi
pour l'analyse des variables gaussiennes.
Un résultat utile concernant la dispersion d'une variable
aléatoire est l'inégalité de Bienaymé-Tchébichev : la probabilité
pour que l'écart à la moyenne soit inférieure à une borne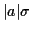 
est minorée par
 |
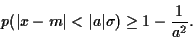(34) |
[ Table des matières ]