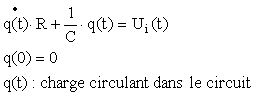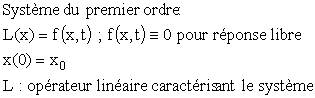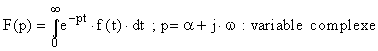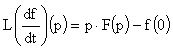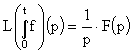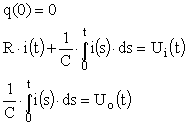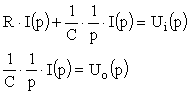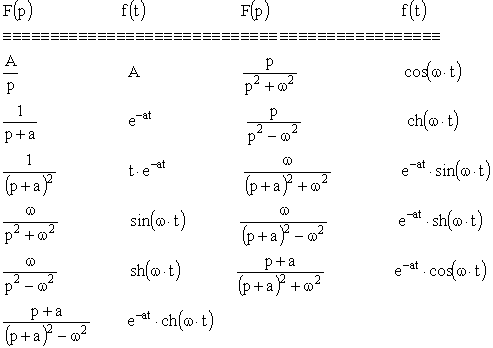______________________________________________________
L'ANALYSE TEMPORELLE
Le but de cette leçon est de présenter les notions de régimes
transitoire, permanent, forcé et libre, ainsi que d'introduire au
calcul opérationnel.
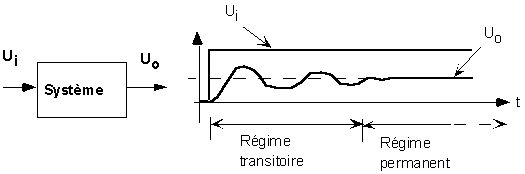
On présente d'abord la distinction classique
entre régime transitoire et régime établi. Pour un
système stable, le régime commence par être transitoire
pendant un temps dépendant de ses caractéristiques, puis
passe dans un régime établi.
Comme l'analyse harmonique se fait toujours en régime établi,
on utilise l'analyse temporelle avec des signaux non-sinusoïdaux pour
étudier les régimes transitoires.
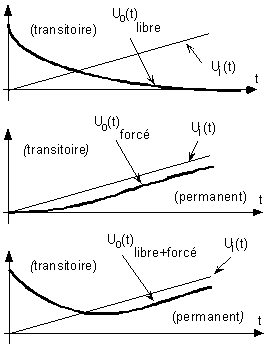
On distingue ensuite le régime libre - correspondant à l'évolution
du système sans excitation, laissé à ses conditions
initiales -, du régime forcé, comme réponse spécifique
du système à son excitation.
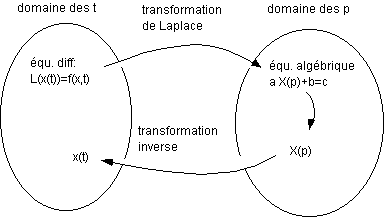
On introduit enfin la transformation de Laplace, qui est un outil souvent
utilisé pour étudier les régimes transitoires, car
il permet de résoudre facilement les équations différentielles
linéaires à coefficients constants.
______________________________________________________
Table des matières
_________________________________________________________________
____________________________________
______________________________________________________
1. REGIME TRANSITOIRE ET
REGIME PERMANENT
_____________
1.1. Définition
1.2. Exemple : Circuit RC
1.1.
Définition
Dans la leçon précédente,
nous avons traité du régime sinusoïdal dit permanent
: on suppose qu'il s'est écoulé suffisamment de temps
depuis l'enclenchement du système, pour que tous les signaux aient
pris un rythme de croisière, c'est-à-dire se retrouvent en
régime permanent. L'analyse temporelle est une méthode complémentaire
à l'analyse harmonique, dans la mesure où elle permet d'étudier
le régime transitoire d'un système.
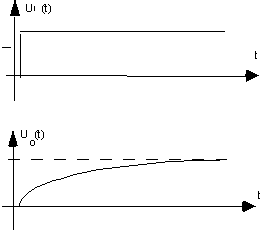
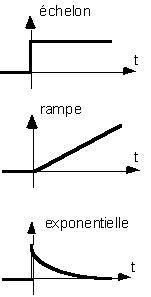
Par exemple, on applique ce qu'on appelle un échelon
unité : une brusque variation de signal d'entrée :
Du point de vue mathématique, on comprend
qu'à la résolution d'une équation différentielle
linéaire, on va obtenir certains termes qui seront amortis par des
exponentielles négatives, et d'autres pas. Ainsi, le régime
transitoire est donné par les termes de la solution qui sont
amortis exponentiellement. Les autres termes définissent ce qu'on
appelle le régime permanent.
1.2.
Exemple : Circuit RC
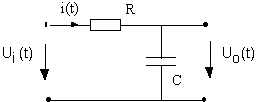
Soit la cellule RC passe-bas :
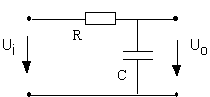
L'application des lois de Kirchhoff et des relations
constitutives des éléments R et C nous procure l'équation
différentielle suivante :
La solution générale de l'équation
homogène est :
La solution particulière est :
La solution générale est :
Représentation graphique de la réponse
indicielle :
______________________________________________________
2. REGIME LIBRE ET REGIME FORCE
_____________
2.1. Définition
2.2. Exemple du circuit RC
2.3. Remarques sur les différents régimes
2.1.
Définition
Parallèlement à la distinction régime
transitoire et permanent, il s'en impose à l'ingénieur une
seconde : le régime libre correspond à l'évolution
du système laissé à lui-même, sans intervention
extérieure. Du point de vue mathématique, cela revient à
laisser agir les seules conditions initiales, sans membre de droite dans
l'équation différentielle ; la réponse libre du système
est la solution à l'équation homogène, avec conditions
initiales :
Le régime forcé correspond
à la réponse du système lorsque ses conditions initiales
sont nulles et qu'il n'y a donc que l'excitation qui agit sur le système.
2.2.
Exemple du circuit RC
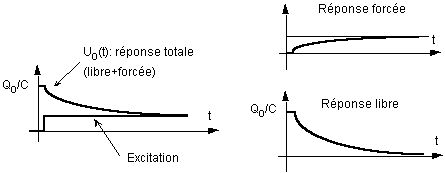
Dans l'exemple précédent du circuit
RC passe-bas, si on a une charge 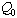 initiale stockée dans la capacité, on obtient :
initiale stockée dans la capacité, on obtient :
Ici le régime libre n'est pas nul, comme
auparavant. La réponse transitoire s'en trouve modifiée,
alors que le régime permanent est le même, vu qu'il dépend
de l'excitation et que cette dernière est encore un échelon
unité.
2.3.
Remarques sur les différents régimes
Le régime libre d'un système linéaire
est transitoire si le système est passif, car il y a toujours amortissement
par pertes d'énergie non compensées.
La réciproque est fausse : le régime
transitoire ne découle pas seulement du régime libre, car
l'excitation du système, qui est déterminante du régime
permanent, produit aussi un régime transitoire.
Par exemple, prenons un système du premier
ordre, avec condition initiale non nulle et excitation en rampe :
______________________________________________________
3. CALCUL OPERATIONNEL:
LA TRANSFORMATION DE LAPLACE
_____________
3.1. Transformation
de Laplace
3.2. Langage
3.3. Quelques propriétés
3.4. Fonction de transfert complexe
3.5. Exemple : Circuit RC passe-bas
3.6. Transformées de Laplace de quelques signaux
3.7. Tables de quelques transformées
Nous présentons ici quelques rudiments
concernant la transformée de Laplace, outil très pratique
pour résoudre les équations différentielles linéaires
à coefficients constants. Ce point trouve donc sa place dans ce
chapitre consacré à l'analyse temporelle de systèmes
linéaires. De plus, on utilise couramment en électronique
la transformée de Fourier, qui est mathématiquement un cas
particulier de celle de Laplace. Cette dernière, est introduite
à la leçon suivante.
3.1.
Transformation de Laplace
On considère f(t) une fonction
dite causale, c'est à dire que f(t)=0 pour t<0. On applique un
opérateur dit de Laplace sur cette fonction f :
La fonction 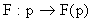 est
la transformée de Laplace de la fonction
est
la transformée de Laplace de la fonction 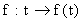 .
.
L'utilité de cette transformation
apparaît immédiatement avec l'exposé de ses principales
propriétés.
3.2.
Langage
F est appelée image de f on écrit
: 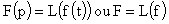
f est appelée original de F on écrit
: 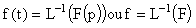
3.3.
Quelques propriétés
La vérification de ces propriétés
ne pose aucun problème, à partir de la définition
même de la transformation de Laplace.
Ces propriétés, particulièrement
les trois premières expriment ceci de remarquable qu'une équation
différentielle linéaire (à coefficients constants)
se transforme, dans l'espace de Laplace, en équation algébrique.
C'est pourquoi cette transformée de Laplace est un outil important
pour les ingénieurs.
3.4.
Fonction de transfert complexe
Nous avons déjà vu, en analyse harmonique,
que le système peut être représenté par un nombre
complexe, dont la phase représente le déphasage induit par
le circuit, et le module le rapport des amplitudes d'entrée et de
sortie. La variable, en analyse harmonique, est le nombre imaginaire.
Avec la transformée de Laplace, on pose
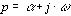 comme variable
complexe, généralisant celle du régime harmonique
(L'introduction de la composante réelle
comme variable
complexe, généralisant celle du régime harmonique
(L'introduction de la composante réelle 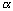 permet l'approche des régimes transitoires). On obtient, pour les
impédances résistives, capacitives et inductives :
permet l'approche des régimes transitoires). On obtient, pour les
impédances résistives, capacitives et inductives :
Ces relations pour les impédances expriment
que la résistance a une caractéristique statique, que la
capacité "intègre" le courant, que l'inductance
"dérive" le courant.
En traitant un circuit à l'aide de cet
outil, les signaux d'entrée et de sortie se transforment en fonctions
complexes et le rapport de ces deux fonctions est encore complexe dans
le cas général : c'est la fonction de transfert du
circuit.
3.5.
Exemple : Circuit RC passe-bas
Soit le circuit RC suivant :
Ses équations temporelles sont données
par :
Après transformation de Laplace, on obtient
:
Soit pour la fonction de transfert complexe :
Nous avons exprimé la fonction de transfert
en régime harmonique de la sorte :
Sur cet exemple, nous voyons bien que l'utilisation
des nombres complexes en régime harmonique représente bel
et bien un cas particulier de l'utilisation de la transformée de
Laplace, où la variable p est réduite à son terme
imaginaire :
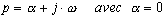 .
.
3.6. Transformées
de Laplace de quelques signaux
3.7.
Tables de quelques transformées
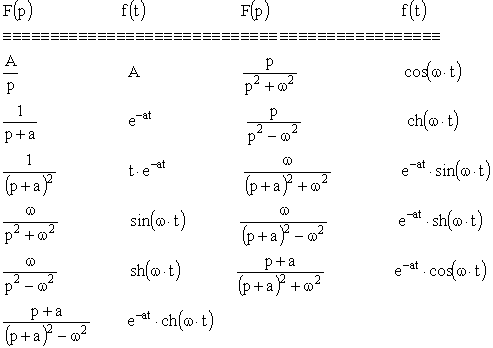
[ Table des matières ]